2 Tema 1. Introducción a los procesos estocásticos
Los procesos estocásticos modelizan cantidades numéricas que cambian con el tiempo de manera aleatoria. Ejemplos del mundo real de estos procesos incluyen:
Resultados sucesivos en un juego de azar.
Número de plazas ocupadas en un parking.
Porcentaje de cielo cubierto en el cielo de Madrid.
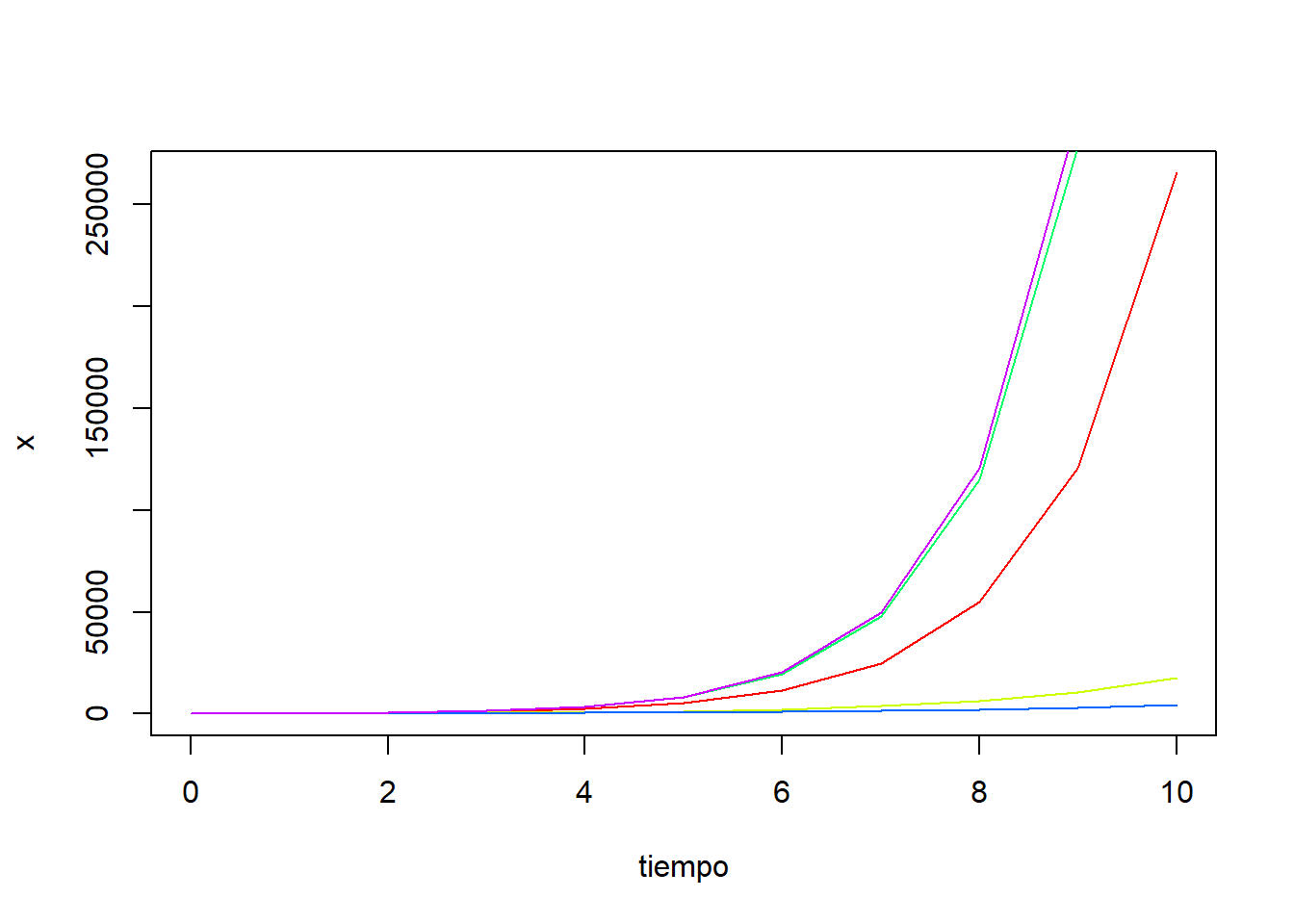
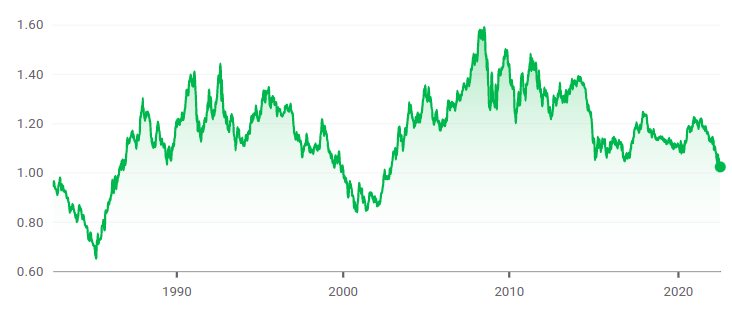
Evolución del precio de activos financieros: acciones, tipos de cambio de divisas o criptomonedas, materias primas, etc.
Indicadores económicos como la inflación, el precio de la luz, y el IBEX 35.
Los procesos estocásticos proporcionan marcos matemáticos para modelar y comprender estos fenómenos, lo que permite hacer predicciones y tomar decisiones informadas.
2.1 Conceptos básicos y ejemplos
A lo largo de este tema, vamos a fijar un espacio de probabilidad \((\Omega,\mathcal{F},\mathbb{P})\) y un subconjunto \(\mathbb{T}\subset [0,\infty)\).
Interpretamos \(t\) como el tiempo (medido en cierta unidad).
Si \(\mathbb{T}\) es contable (por ejemplo, \(\mathbb{T}=\{0<1<2<\ldots\}\), diremos que el proceso estocástico \((X_t)_{t\in\mathbb{T}}\) es de tiempo discreto.
Si \(\mathbb{T}\) es un intervalo (por ejemplo, \(\mathbb{T}=[0,T]\) o \(\mathbb{T}=[0,\infty)\), diremos que el proceso estocástico es de tiempo continuo.
Para cada \(t\in\mathbb{T}\) tenemos una variable aleatoria \(X_t\). La variable aleatoria \(X_t\) tomará un valor numérico \(X_t(\omega)\) para cada \(\omega\in\Omega\). A los posibles valores que toma un proceso estocástico se les llama estados.
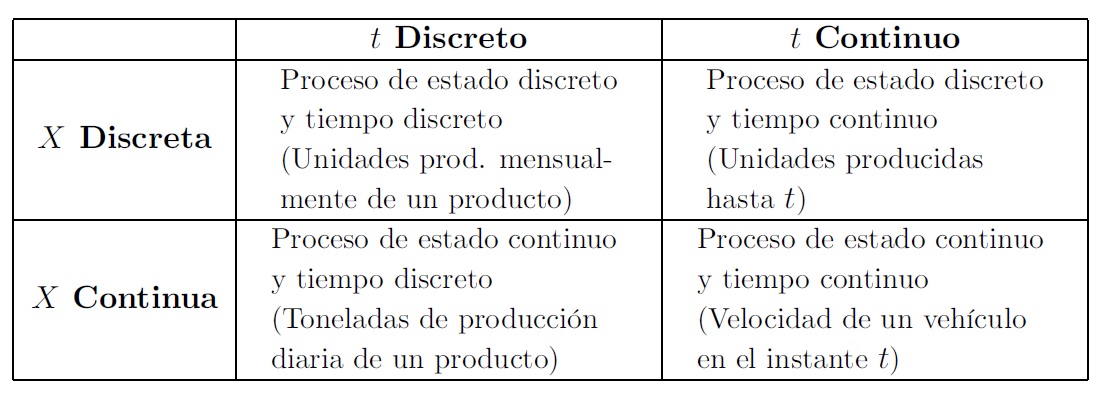
Si para cada \(t\in \mathbb{T}\) la variable aleatoria \(X_t\) es de tipo discreto, diremos que el proceso estocástico \((X_t)_{t\in\mathbb{T}}\) es de estado discreto.
Si para cada \(t\in \mathbb{T}\) la variable aleatoria \(X_t\) es de tipo continuo, diremos que el proceso estocástico \((X_t)_{t\in\mathbb{T}}\) es de estado continuo.
En lo que sigue, siempre supondremos que \(0\in\mathbb{T}\). Esta condición no es realmente restrictiva, ya que podemos desplazar el tiempo por una constante para garantizar que dicha condición se cumpla.
- Para un proceso estocástico \((X_{t})_{t=0,1,2,\ldots}\) de tiempo discreto, cada trayectoria define una sucesión de números reales \((x_t)_{t=0,1,2,\ldots}\).
- Para un proceso estocástico \((X_{t})_{t\in [0,\infty)}\) de tiempo continuo, cada trayectoria define una función real \(t\mapsto x(t)\colon [0,\infty)\to\mathbb{R}\).
Cada trayectoria corresponde a una observación particular de la evolución del valor de un proceso estocástico en el tiempo.
Ejemplo
Supón que inviertes 100 euros en una cuenta bancaria con tipo de interés anual \(R\), compuesto anualmente. Es decir, si \(X_t\) es la cantidad de dinero en el año \(t\), entonces \[ X_t=100\cdot(1+R)^t\quad\mbox{ para }t=0,1,2,\ldots. \] Supongamos también que el valor de \(R>0\) es fijado cuando metes el dinero en la cuenta y sigue una distribución \(\mathrm{Exp}(1)\).
Para cada observación particular \(R=r\) de la variable \(R\) tendremos una trayectoria del proceso estocástico \((X_t)_{t=0,1,2,\ldots}\). Podemos simular y dibujar cinco trayectorias de este proceso estocástico mediante el siguiente código en R:
set.seed(112)
nsim <- 5
r <- rexp(nsim, 1)
tiempo <- 0:10
x <- 100*(1+r[1])^tiempo
colores <- rainbow(nsim)
plot(tiempo, x, col=colores[1], type = "l", lty = 1)
for(i in 2:nsim){
x <- 100*(1+r[i])^tiempo
lines(tiempo, x, col=colores[i])
}
El proceso del ejemplo anterior es un caso particular de un tipo de proceso el cual introducimos a continuación.
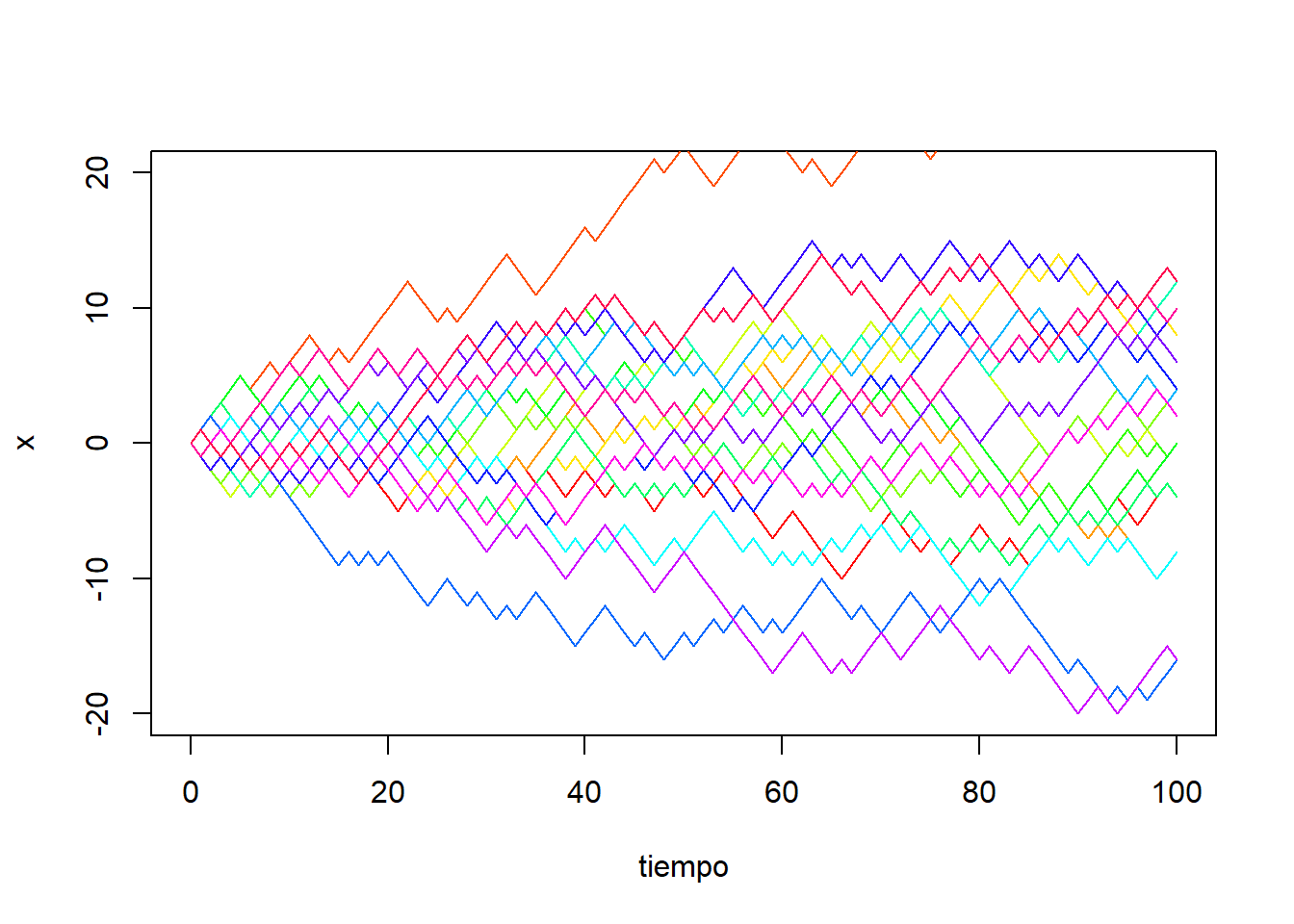
Para cada secuencia de lanzamientos observados, tendremos una trayectoria diferente del proceso estocástico \((X_t)_{t=0,1,2,\ldots}\). Podemos simular y dibujar veinte trayectorias de este proceso estocástico mediante el siguiente código en R:
set.seed(145)
nsim <- 20
nlanzamientos <- 100
y <- sample(c(-1,1), size=nlanzamientos, replace=TRUE)
x <- c(0, cumsum(y))
tiempo <- 0:nlanzamientos
colores <- rainbow(nsim)
plot(tiempo, x, col=colores[1], type = "l", lty = 1, ylim=c(-20, 20))
for(i in 2:nsim){
y <- sample(c(-1,1), size=nlanzamientos, replace=TRUE)
x <- c(0, cumsum(y))
lines(tiempo, x, col=colores[i])
}
2.2 Funciones de distribución asociadas a un proceso
Dado un proceso estocástico \((X_t)_{t\in\mathbb{T}}\), cada variable aleatoria \(X_t\) tendrá su propia distribución de probabilidad la cual puede ser discreta o continua. Observar un proceso estocástico en un solo tiempo de forma aislada no es útil para describir su comportamiento como función del tiempo, ya que los valores observados en un tiempo pueden condicionar su comportamiento en tiempos distintos. Por ejemplo, en el caso del camino aleatorio simétrico en el que apostamos un euro a cara, si hemos acumulado muchas ganancias en el pasado, la ganancia acumulada seguirá siendo alta en las siguientes jugadas, ya que partimos de una cantidad alta la cual disminuirá a lo sumo en un euro en cada lanzamiento.
Por ese motivo, es necesario estudiar la distribución de probabilidad conjunta a lo largo de varios tiempos.
La función de distribución finito dimensional describe el comportamiento probabilístico del proceso estocástico observado en los distintos tiempos \(t_1,t_2,\ldots,t_n\). La distribución de probabilidad de un proceso está caracterizada por el conjunto de todas las distribuciones finito dimensionales. En particular, dos procesos estocásticos con las mismas funciones de distribución finito dimensionales tendrán un comportamiento probabilístico similar.
En el caso de que \((X_t)_{t\in\mathbb{T}}\) sea de estado discreto, entonces dicho comportamiento probabilístico puede ser descrito por medio la función puntual de probabilidad finito dimensional \[ P_{t_1,t_2,\ldots,t_n}(x_1,x_2,\ldots,x_n)=\mathbb{P}(X_{t_1}=x_1, X_{t_2}=x_2,\ldots,X_{t_n}= x_n). \] En el caso de que \((X_t)_{t\in\mathbb{T}}\) sea de estado continuo, consideraremos la función de densidad finito dimensional \(f_{t_1,t_2,\ldots,t_n}(x_1,x_2,\ldots,x_n)\), la cual verifica \[ \mathbb{P}(a_1<X_{t_1}<b_1,\ldots,a_n<X_{t_n}<b_n)=\int_{a_n}^{b_n}\cdots \int_{a_1}^{b_1}f_{t_1,t_2,\ldots,t_n}(x_1,x_2,\ldots,x_n) {\mathrm dx_1}\ldots {\mathrm dx_n} \] para todo \(-\infty\le a_i<b_i\le \infty\).
Para un proceso estocástico \((X_{t})_{t=0,1,2,\ldots}\) de tiempo discreto, la función media define una sucesión de números reales \((\mu_X(t))_{t=0,1,2,\ldots}\).
Para un proceso estocástico \((X_{t})_{t\in [0,\infty)}\) de tiempo continuo, la función media define una función real \(t\mapsto \mu_X(t)\colon [0,\infty)\to\mathbb{R}\).
La función de medias da una idea de cómo el proceso estocástico se comporta en promedio a lo largo del tiempo.
2.3 Procesos estacionarios y débilmente estacionarios
Los procesos estocásticos se pueden dividir entre estacionarios (en sentido estricto), débilmente estacionarios y no estacionarios. Intuitivamente hablando, un proceso estocástico es estacionario (en sentido estricto) si su comportamiento probabilístico o distribución no cambia con el tiempo.
En particular, si un proceso es estacionario, entonces todas las variables aleatorias \(X_t\) del proceso tienen la misma distribución, es decir, están idénticamente distribuidas. Esto no implica que los vectores aleatorios que se pueden formar con las variables del proceso en diferentes instantes tengan todos la misma distribución.
En la práctica es muy útil saber si un proceso estocástico es estacionario cuando es necesario predecir el comportamiento futuro de dicho proceso. Si sabemos que el proceso es estacionario, entonces observando su comportamiento en el pasado podremos inferir información de su comportamiento en el futuro.
A continuación introducimos una noción de estacionaridad menos exigente, la cual es también muy útil para predecir comportamientos futuros de procesos estocásticos reales.
Obsérvese que, en particular, si el proceso es débilmente estacionario tendrá función de varianzas constante.
Dado que la media \(\mu_X(t)\) es determinada por la función de distribución marginal \(F_t(x)\), y la covarianza \(C_X(s,t)\) es determinada por la función de distribución marginal \(F_{s,t}(x)\), todo proceso estacionario será también débilmente estacionario. Sin embargo, es posible que un proceso sea débilmente estacionario pero no estacionario.
2.4 Procesos gaussianos
A continuación introducimos una de las familias de procesos estocásticos más importantes: los procesos gaussianos. Este tipo de procesos tienen importantes aplicaciones en Machine Learning.
Recordemos primero la noción de variable Normal multivariante. Una propiedad importante de las variables normales multivariadas es que su función de densidad (y, por tanto, su distribución) está completamente determinada por el vector de medias y la matriz de covarianzas.
Otra importante propiedad de las variables aleatorias normales multivariadas que conviene recordar es que las transformaciones lineales de estas variables también son normales multivariadas. En otras palabras, si \(\vec{X}\) es un vector aleatorio Normal multivariante de tamaño n, \(A\) es una matriz constante de tamaño \(m\times n\), y \(\vec{b}\) es un vector constante de tamaño \(m\), entonces el vector aleatorio \(\vec{Y}=A\vec{X}+\vec{b}\) también es un vector aleatorio Normal multivariante.
Una importante propiedad de los procesos gaussianos es que las nociones de estacionaridad y estacionaridad débil son equivalentes para este tipo de procesos. En la práctica esto significa que para verificar que un proceso gaussiano es estacionario basta analizar su media y covarianza. Concretamente, tenemos lo siguiente.
2.5 Ejemplos y simulación
En lo que sigue vamos a estudiar y simular en R algunos ejemplos particulares de procesos estocásticos gaussianos, analizando en cada caso si se trata de procesos estacionarios o no estacionarios.
2.5.1 Ruido blanco gaussiano
Un proceso estocástico \((X_{t})_{t\in\mathbb{T}}\) se llama ruido blanco gaussiano si las variables aleatorias \(X_t\) son independientes y siguen una distribución \(N(0,\sigma^2)\).
Claramente el ruido blanco gaussiano es un proceso gaussiano. Además, \(\mu_X(t)=0\), \(C_X(t,s)=0\) si \(t\neq s\), y \(C_X(t,t)=\sigma^2\). Lo cual en particular implica que el ruido blanco gaussiano es un proceso estacionario.
Podemos simular en R un trayectoria del ruido blanco gaussiano:
set.seed(11)
sigma <- 1
tiempos = seq(from = 0, to = 1, by = 0.001)
x=rnorm(length(tiempos), 0, sigma)
plot(tiempos, x, type = "l", lty = 1)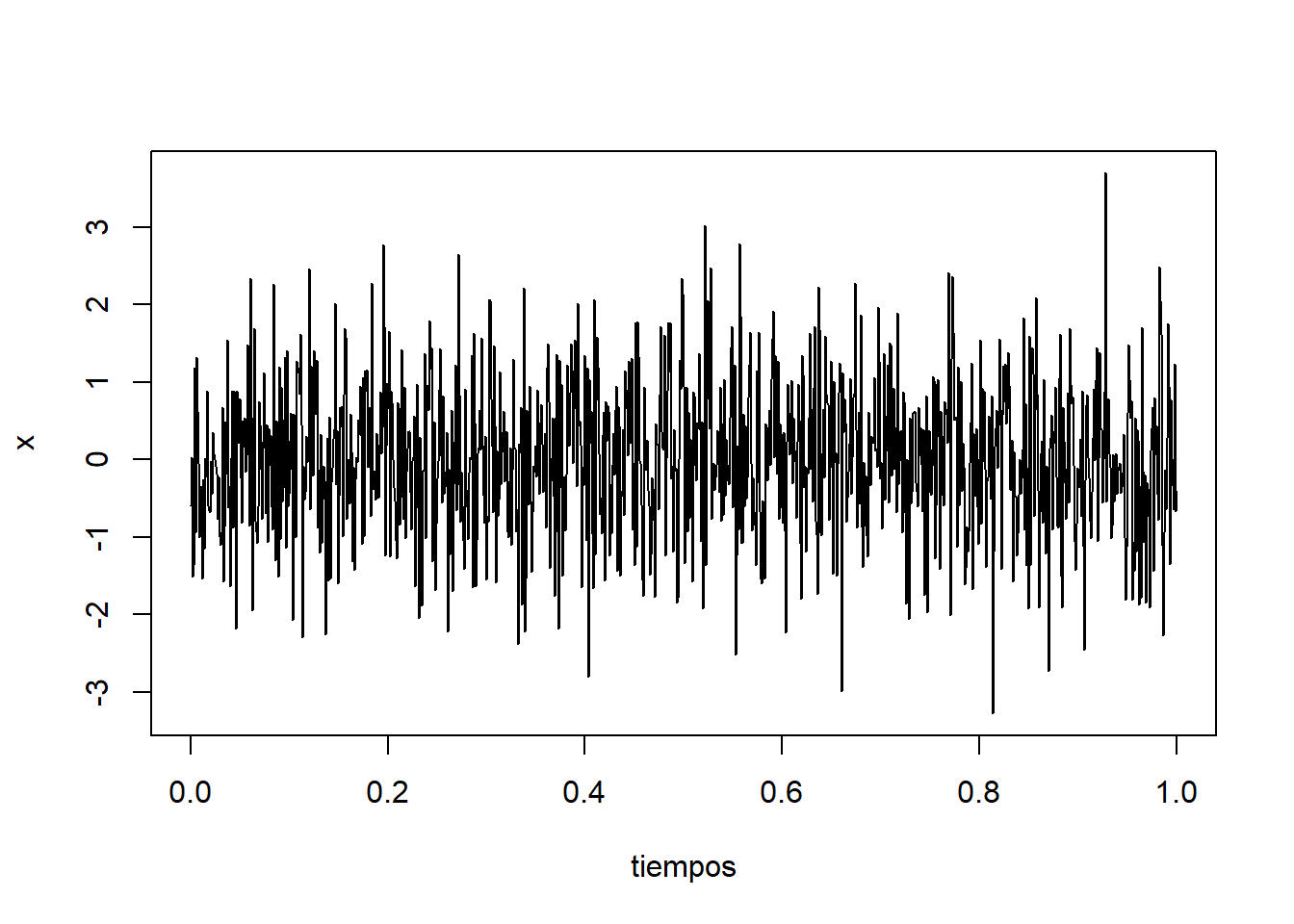
Obtenemos una trayectoria extremadamente irregular. Además, observamos a simple vista un comportamiento estacionario del proceso.
2.5.2 Movimiento Browniano
Un proceso estocástico \((X_{t})_{t\in [0,\infty)}\), de tiempo continuo, se dice que es un movimiento Browniano o proceso de Wiener si:
\(X_0=0\),
Para todo par de tiempos \(s\le t\), la variable aleatoria \(X_{t}-X_{s}\) sigue una distribución \(N(0,t-s)\),
Para cualquier sucesión de tiempos \(t_1<t_2<\ldots<t_n\) se tiene que las variables aleatorias \[ X_{t_2}-X_{t_1},\quad X_{t_3}-X_{t_2},\quad \ldots,\quad X_{t_n}-X_{t_{n-1}} \] son independientes.
Las trayectorias \(t\mapsto X_t(\omega)\) son funciones continuas.
El movimiento Browniano se utiliza en finanzas para modelar la evolución del precio de activos financieros como las acciones o los tipos de cambio. En particular, se aplica a la valoración de opciones financieras mediante el modelo de Black-Scholes, y el análisis de riesgos.
A continuación vamos a simular una trayectoria del movimiento Browniano. Para ello fijamos un incremento de tiempo \(\Delta t>0\) y un número natural \(n\). Deseamos simular una trayectoria en los instantes de tiempo \(t_0=0\), \(t_1=\Delta t\), …, \(t_n=n\Delta t\). En vista de la definición de movimiento Browniano, tenemos que los incrementos \[ \Delta X_{t_1}=X_{t_1}-X_{t_0},\quad \Delta X_{t_2}=X_{t_2}-X_{t_1},\quad ...,\quad \Delta X_{t_n}=X_{t_n}-X_{t_{n-1}}, \] son variables aleatorias idependientes y siguen todas ellas una distribución \(N(0,\Delta t)\). De este modo, nuestra estrategia será simular los valores de los incrementos mediante la generación de una muestra aleatoria de \(n\) variables \(N(0,\Delta t)\) independientes, y reconstruir la trayectoria del proceso a partir de dichos incrementos. Esto podemos lograrlo mediante el siguiente código de R:
set.seed(11)
n <- 1000
dt <- 1/n
tiempo <- seq(from=0, to=1, by=dt)
incrementos <- rnorm(n, 0, sqrt(dt))
x <- c(0, cumsum(incrementos))
plot(tiempo, x, type = "l", lty = 1)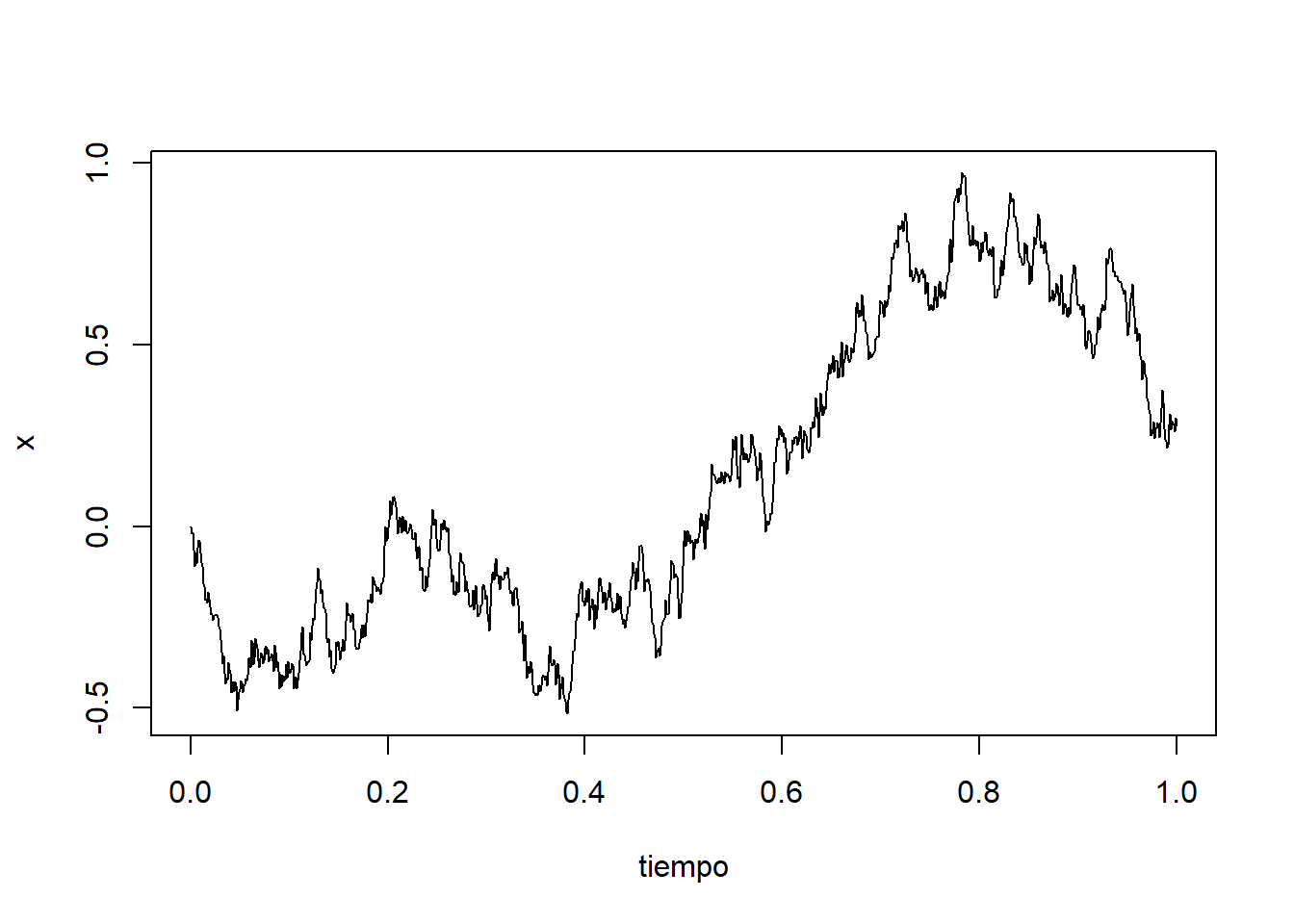
Para analizar el comportamiento probabilístico, simularemos diez trayectorias del proceso:
set.seed(123)
nsim <- 10
n <- 1000
dt <- 1/n
tiempos <- seq(from=0, to=1, by=dt)
incrementos <- rnorm(n, 0, sqrt(dt))
x <- c(0, cumsum(incrementos))
colores <- rainbow(nsim)
plot(tiempos, x, ylim=c(-2,2), type = "l", lty = 1, col=colores[1])
for(i in 2:nsim){
incrementos=rnorm(n, 0, sqrt(dt))
x <- c(0, cumsum(incrementos))
lines(tiempos, x, col=colores[i])
}
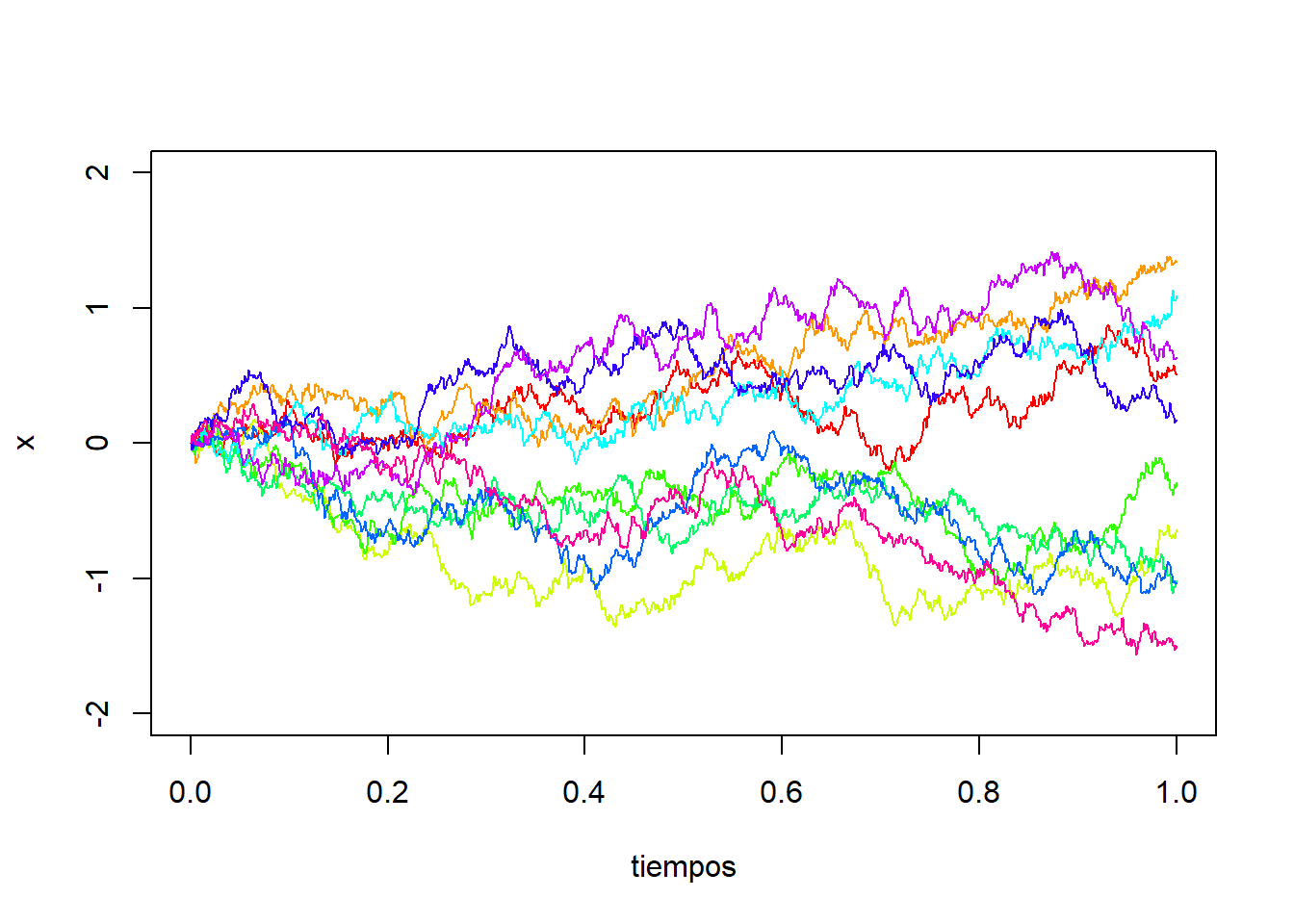
A simple vista observamos un comportamiento no estacionario del proceso. Notamos que a medida que avanza el tiempo, las trayectorias tienden a volverse más dispersas, lo que indica que el comportamiento probabilístico de las trayectorias varía con el tiempo.
El movimiento Browniano es un proceso gaussiano. De hecho, la distribución de probabilidad del vector aleatorio \((X_{t_1},X_{t_2},\ldots,X_{t_n})\), para \(t_1<t_2<\ldots<t_n\), es normal multivariada porque se obtiene como una transformación lineal del vector \((X_{t_1},X_{t_2}-X_{t_1},\ldots,X_{t_n}-X_{t_{n-1}})\), el cual es normal multivariado porque sus componentes son independientes y normales. ¿Puedes encontrar dicha transformación lineal?.
Además, \(\mu_X(t)=\mathbb{E}(X_t)=0\) y, para \(s\le t\), \[\begin{align*} C_X(s,t)&=\mathbb{E}\Big(X_s X_t\Big)\\ &=\mathbb{E}\Big(X_s (X_t-X_s + X_s)\Big)\\ &=\mathbb{E}\Big(X_s(X_t-X_s)\Big) + \mathbb{E}\Big(X_s^2\Big)\\ &=s=\min(s,t). \end{align*}\] En resumen, el movimiento Browniano es un proceso gaussiano con funciones de media y covarianza \(\mu_X(t)=0\), y \(C_X(s,t)=\min(s,t)\), respectivamente. En particular, observamos que este proceso no es estacionario (ni siquiera en el sentido débil), ya que en general no se verifica que \(C_X(s,t)=C_X(0,t-s)\). Por ejemplo, \(C_X(3,4)=\min(3,4)=3\); sin embargo, \(C_X(0,4-3)=\min(0,1)=0\).
A continuación vamos a detallar otra estrategia para simular el movimiente Browniano, la cual se basa en que dicho proceso es gaussiano. Aunque nos vamos a centrar en el caso particular del movimiento Browniano, este procedimiento sirve para simular cualquier proceso gaussiano conocidas sus funciones de media y covarianza. Fijados los tiempos \(t_1<\ldots<t_n\) sabemos que el vector aleatorio \((X_{t_1},X_{t_2},\ldots,X_{t_n})\) sigue una distribución multivariada de media \(\mu_X=0\) y matriz de convarianzas \(C_X=(c_{i,j})_{n\times n}\) donde \(c_{i,j}:=\min\{t_i,t_j\}\). De esta manera, podremos simular una trayectoria mediante la obtención de una muestra aleatoria del anterior vector aleatorio. Para ello utilizamos la libreria mvtnorm de R, la cual permite simular variables aleatorias normales multivariadas:
set.seed(23)
n <- 1000
dt <- 1/n
tiempo = seq(from=0, to=1, by=dt)
# Definimos la matriz de covarianzas
C <- matrix(NA, nrow = n, ncol = n)
C <- dt*pmin(row(C),col(C))
# Simulamos una normal multivariada
library(mvtnorm)
x <- rmvnorm(1, sigma=C)
# Añadimos el valor 0 inicial
x <- c(0, x)
plot(tiempo, x, type = "l", lty = 1)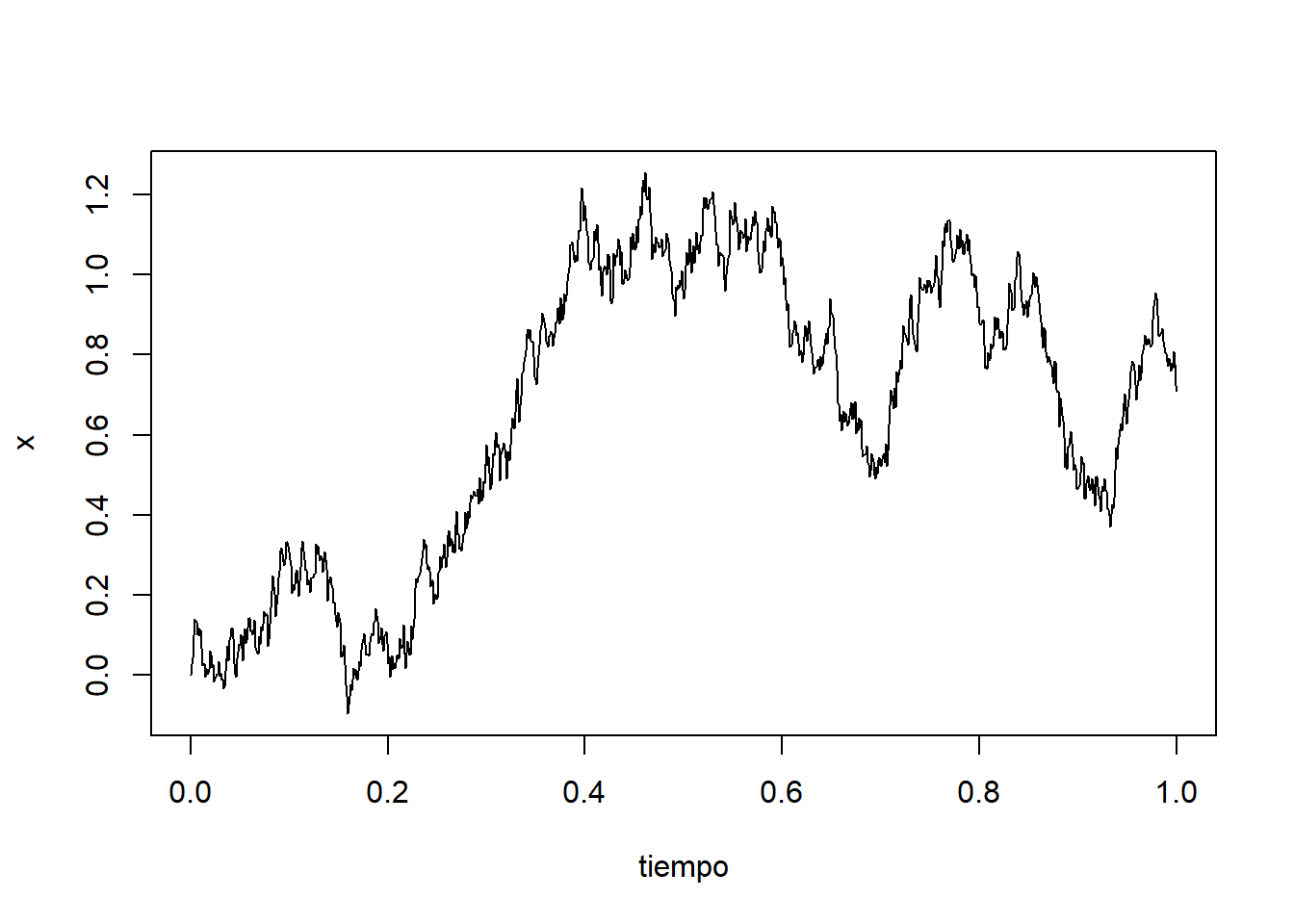
2.5.3 Procesos gaussianos estacionarios isotrópicos
Un tipo particular de proceso gaussiano estacionario son los procesos gaussianos estacionarios isotrópicos. Decimos que un proceso gaussiano estacionario \((X_t)_{t\in\mathbb{T}}\) es isotrópico si su función de medias es constante, \(\mu_X(t)=\mu\), y la función de covarianza depende sólo de la distancia \(|t-s|\), es decir,
\[
C_X(s,t)=K(|t-s|)
\] para cierta función \(K\colon [0,\infty)\to [0,\infty)\) llamada núcleo.
Tomemos por ejemplo \(\mu_X(t)=0\) y el núcleo exponencial cuadrático \(K_l(x):=\exp(-x^2/2l^2)\), donde \(l\) es un parámetro de escala. Vamos a simular en R una trayectoria de dicho proceso:
set.seed(112)
n <- 1000
dt <- 1/n
tiempo <- seq(from=0, to=1, by=dt)
# Definimos la matriz de covarianzas
l <- 1
C <- matrix(NA, nrow = n+1, ncol = n+1)
C <- dt*abs(row(C)-col(C))
C <- exp(-C^2/(2*l^2))
# Simulamos una normal multivariada
library(mvtnorm)
x <- rmvnorm(1, sigma=C)
plot(tiempo, x, type = "l", lty = 1)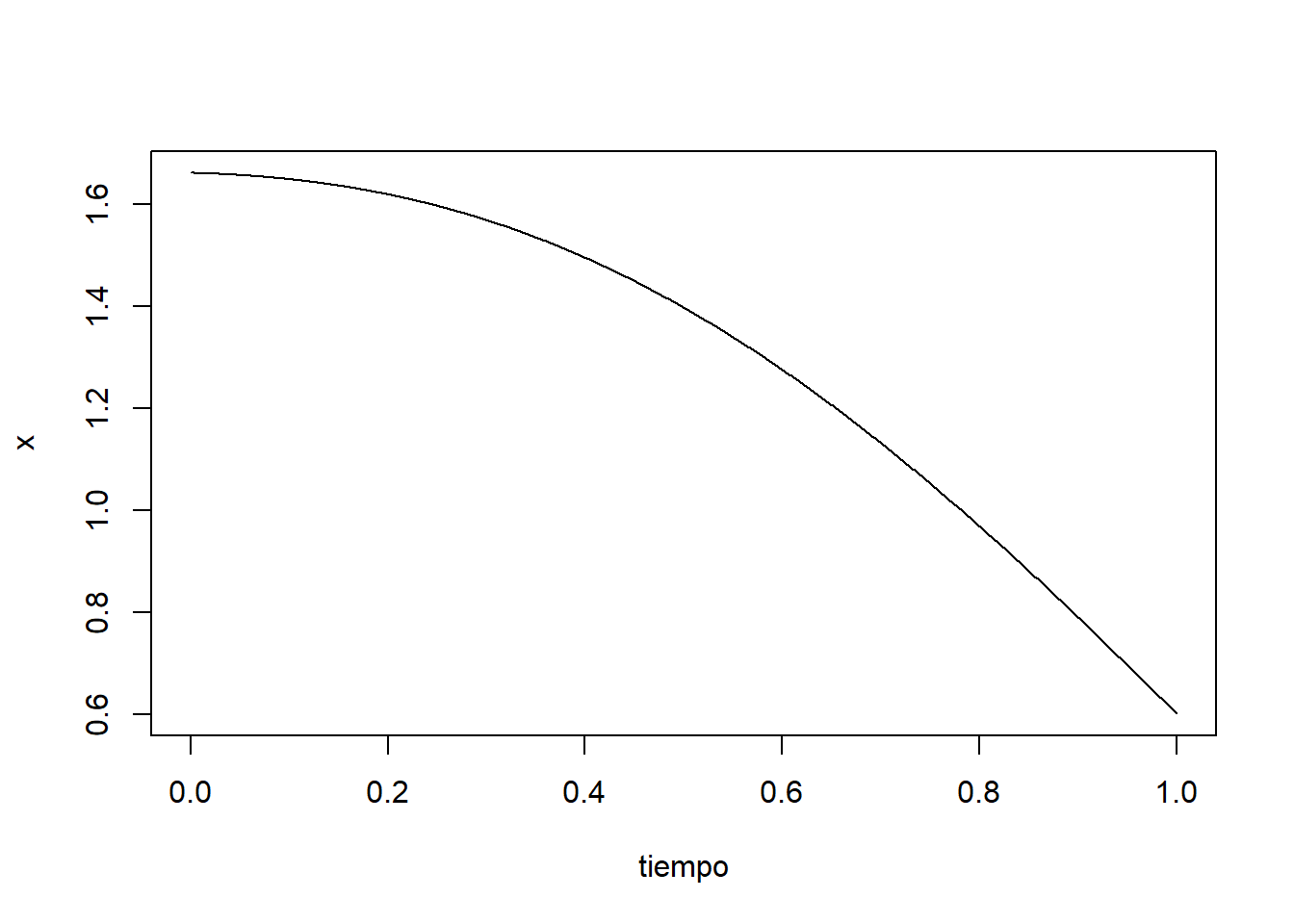
Para analizar el comportamiento probabilístico, podemos simular diez trayectorias del proceso:
set.seed(112)
nsim <- 10
n <- 1000
dt <- 1/n
tiempo <- seq(from=0, to=1, by=dt)
# Definimos la matriz de covarianzas
l <- 1
C <- matrix(NA, nrow = n+1, ncol = n+1)
C <- dt*abs(row(C)-col(C))
C <- exp(-C^2/(2*l^2))
# Simulamos una normal multivariada
library(mvtnorm)
x <- rmvnorm(1, sigma=C)
colores <- rainbow(10)
plot(tiempo, x, type = "l", lty = 1, ylim=c(-2.5,2.5), col=colores[1])
for(i in 2:nsim){
x <- rmvnorm(1,sigma=C)
lines(tiempo, x, col=colores[i])
}
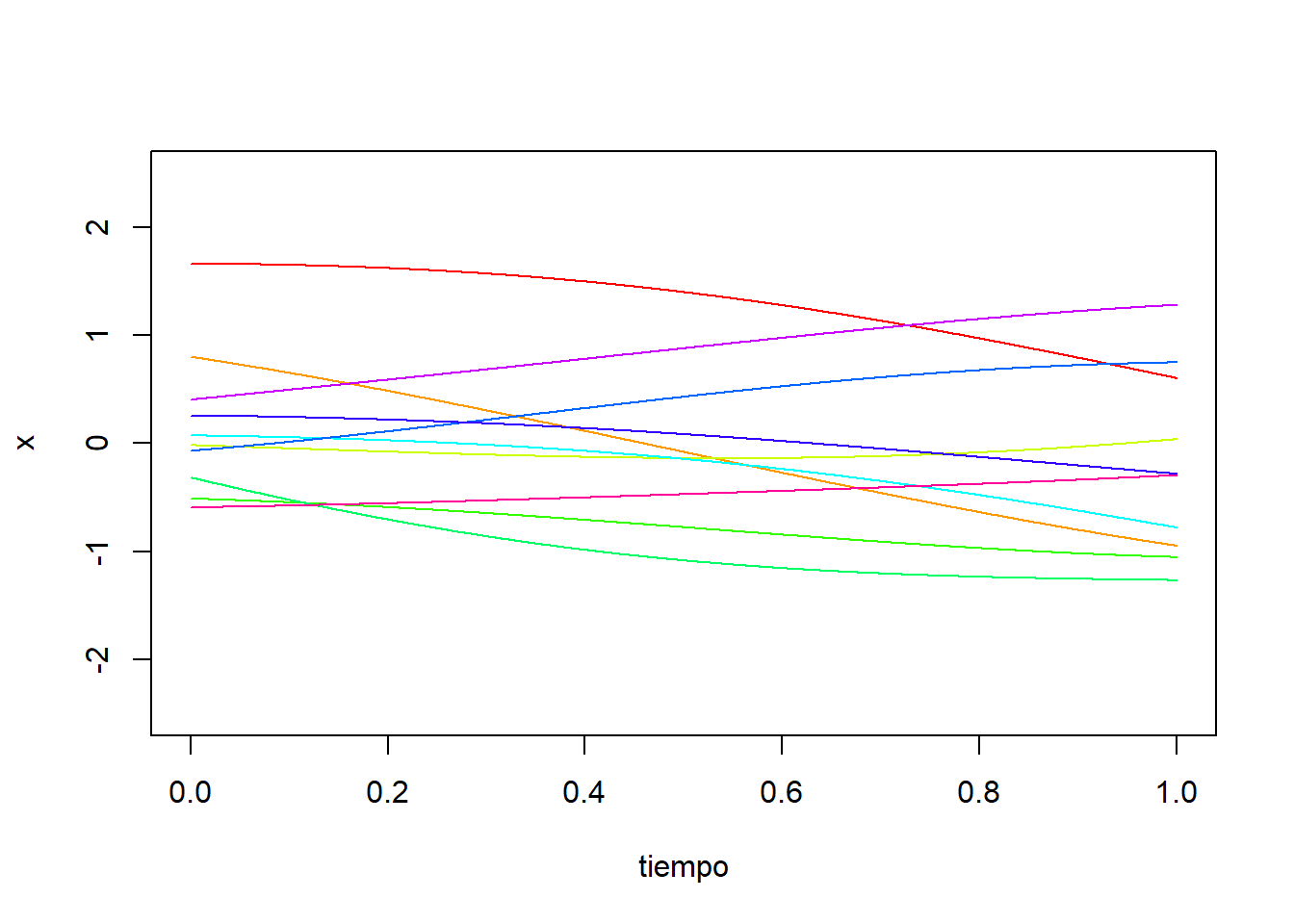
A diferencia del movimiento Browniano, vemos que las trayectorias presentan un comportamiento estacionario, ya que su distribución es la misma a lo largo del tiempo. Otra diferencia con el movimiento Browniano es que las trayectorias tienen una apariencia suave.
Podemos cambiar el parámero de escala, tomando \(l=0.1\). De este modo obtenemos las trayectorias:
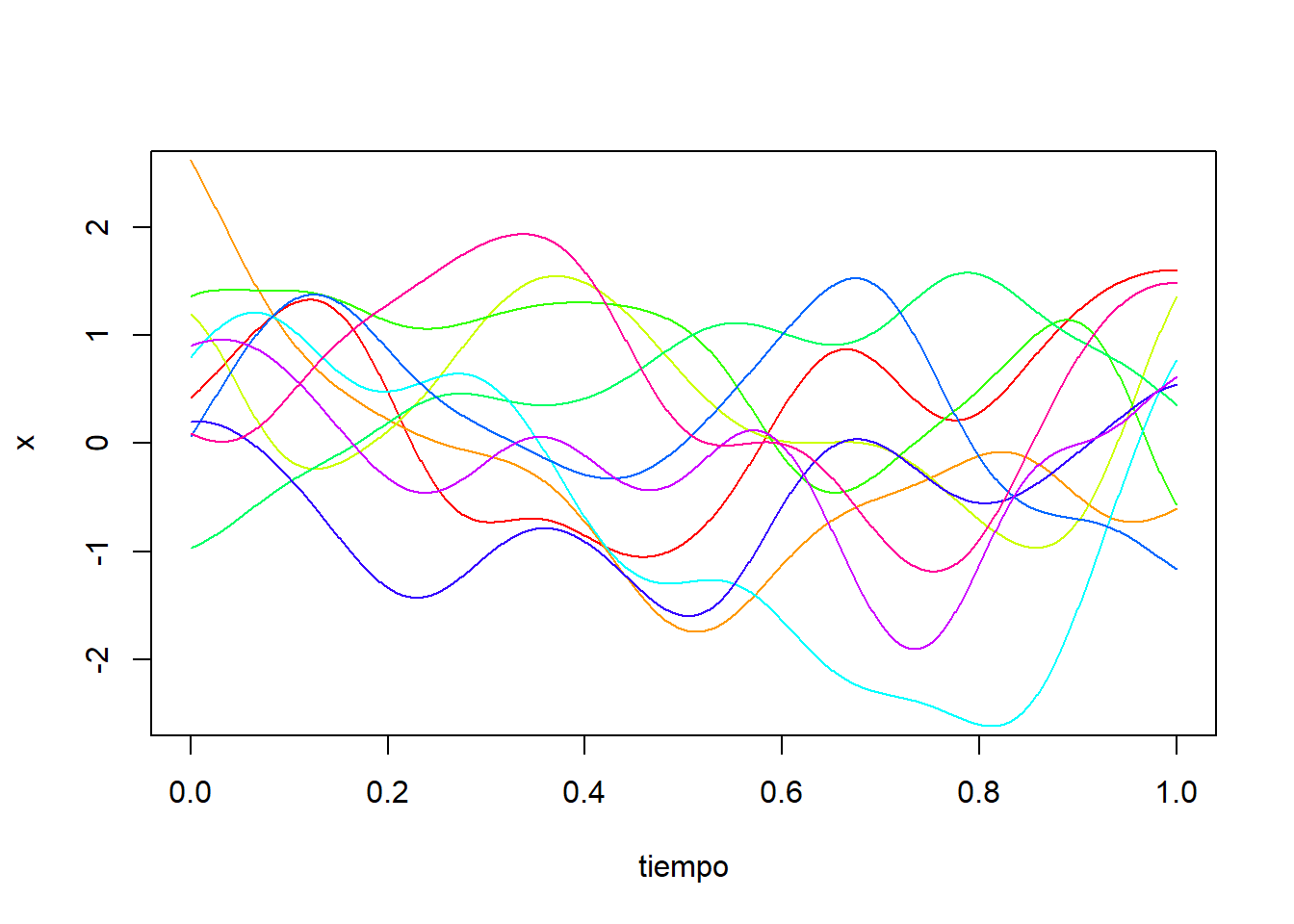
Tomemos ahora el núcleo de Ornstein–Uhlenbeck \(K_l(x):=\exp(-|x|/l)\).
Simulemos algunas trayectorias en R:
set.seed(114)
nsim <- 10
n <- 1000
dt <- 1/n
tiempo <- seq(from=0, to=1, by=dt)
# Definimos la matriz de covarianzas
l <- 1
C <- matrix(NA, nrow = n+1, ncol = n+1)
C <- dt*abs(row(C)-col(C))
C <- exp(-C/l)
# Simulamos una normal multivariada
library(mvtnorm)
x <- rmvnorm(1, sigma=C)
colores <- rainbow(10)
plot(tiempo, x, type = "l", lty = 1, ylim=c(-2.5,2.5), col=colores[1])
for(i in 2:nsim){
x <- rmvnorm(1,sigma=C)
lines(tiempo, x, col=colores[i])
}
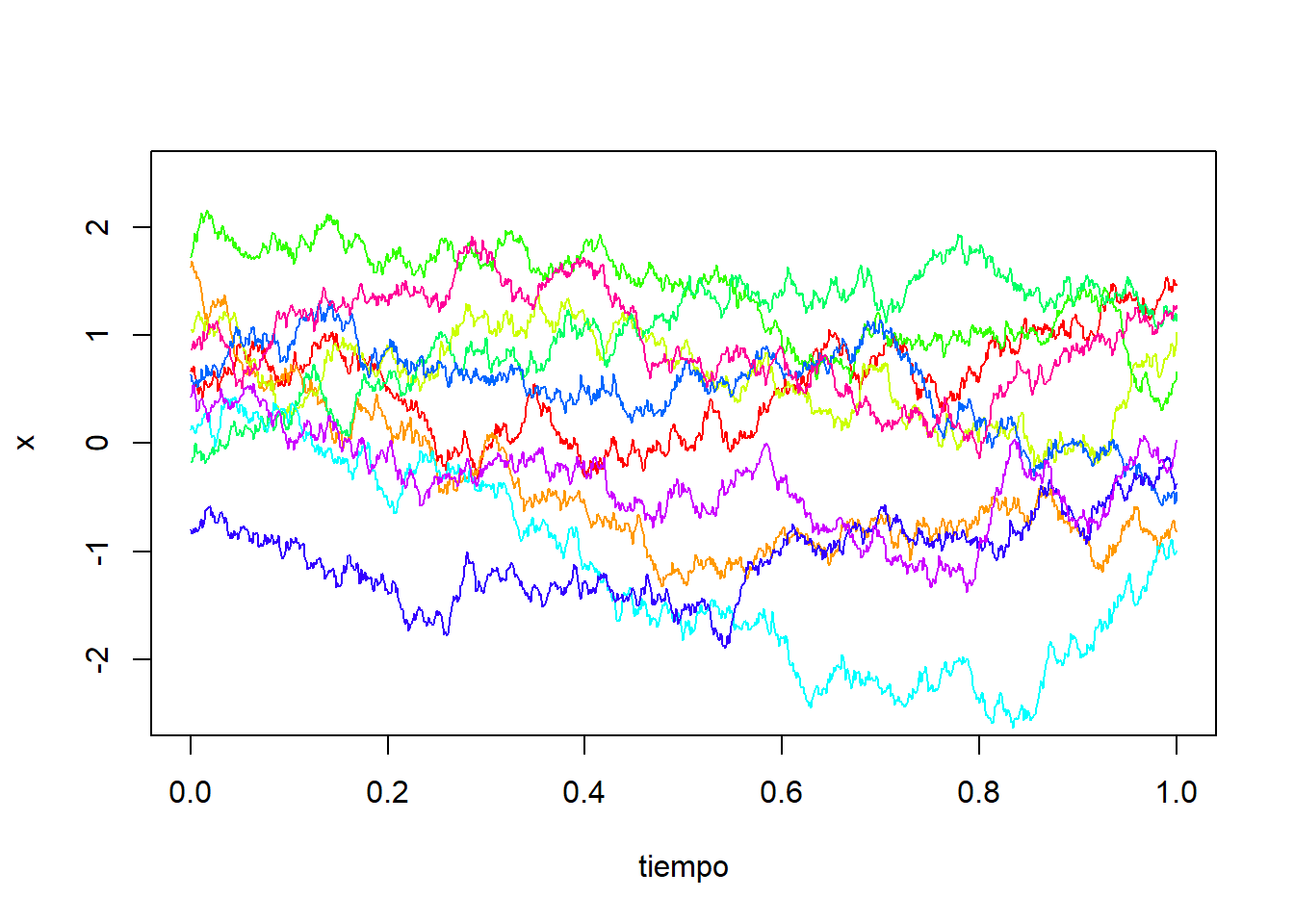
Vemos que las trayectorias tienen una apariencia más irregular la cual nos recuerda al movimiento Browniano. Sin embargo, en este caso tenemos un proceso estacionario cuyas trayectorias se comportan de manera similar a lo largo del tiempo.
2.5.4 Movimiento Browniano fraccional
Otro proceso gaussiano importante es el movimiento Browniano fraccional, el cual es una generalización del movimiento Browniano clásico. A diferencia de éste, los incrementos del movimiento Browniano fraccional no son independientes.
Dado un número \(H \in (0,1)\), decimos que un proceso estocástico \((X_t)_{t\in [0,\infty)}\) es un movimiento Browniano fraccional con índice de Hurst \(H\) si es un proceso gaussiano, su función de medias es constantemente cero, \(\mu_X(t)=0\), y su función de covarianzas está dada por \[ C_X(s,t) = \frac{1}{2}\left( t^{2H} + s^{2H} - |t-s|^{2H} \right). \] El índice de Hurst \(H\) describe la irregularidad del movimiento resultante: valores más altos producen trayectorias más suaves. Este proceso fue introducido por Mandelbrot y Van Ness (1968) para modelizar fenómenos como los mercados financieros.
- Cuando \(H = \tfrac{1}{2}\), el proceso coincide con el movimiento Browniano usual.
- Cuando \(H > \tfrac{1}{2}\), los incrementos están positivamente correlados.
- Cuando \(H < \tfrac{1}{2}\), los incrementos están negativamente correlados.
Vamos a simular en R una trayectoria de dicho proceso para H=0.2:
set.seed(23)
n <- 1000
dt <- 1/n
tiempo = seq(from=0, to=1, by=dt)
# Definimos la matriz de covarianzas para H=0.2
H <- 0.2
C <- matrix(NA, nrow = n, ncol = n)
C <- (1/2)*((dt*row(C))^(2*H) + (dt*col(C))^(2*H) - abs(row(C) - col(C))^(2*H))
# Simulamos una normal multivariada
library(mvtnorm)
x <- rmvnorm(1, sigma=C)
# Añadimos el valor 0 inicial
x <- c(0, x)
plot(tiempo, x, type = "l", lty = 1)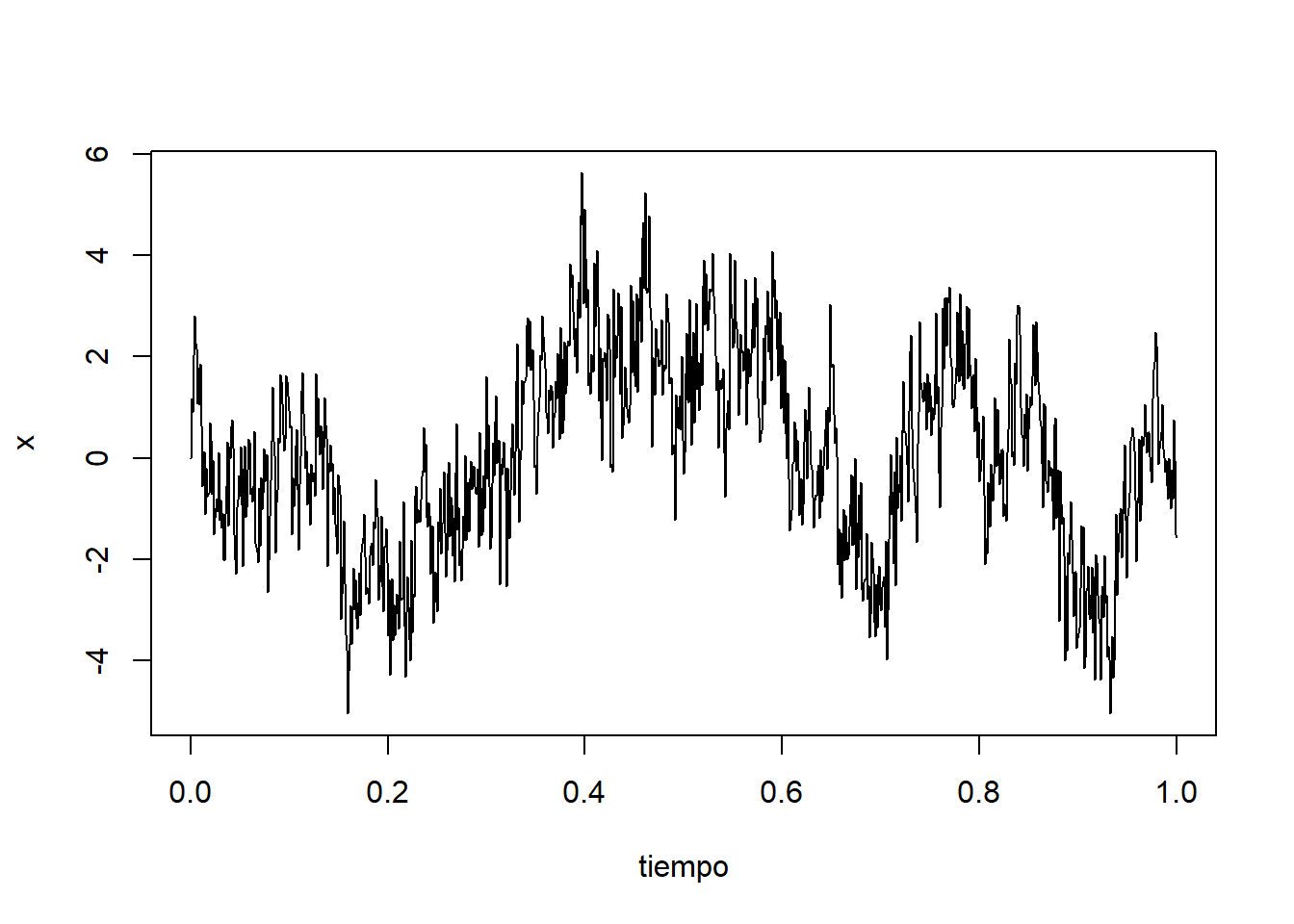
Vemos que la trayectoria obtenida menos suave que en el caso del movimiento Browniano usual. Al igual que el movimiento Browniano usual, no es un proceso estacionario.